Growth rates and nitrate uptake of co-occurring red-tide dinoflagellates Alexandrium affine and A. fraterculus as a function of nitrate concentration under light-dark and continuous light conditions

Article information

Algae. 2019;34(3):237-251

Publication date (electronic) : 2019 September 15

doi : https://doi.org/10.4490/algae.2019.34.8.28

Kyung Ha Lee ¹^,^a, Hae Jin Jeong ¹^,²^,, Hee Chang Kang ¹, Jin Hee Ok ¹, Ji Hyun You ¹, Sang Ah Park ¹

¹School of Earth and Environmental Sciences, College of Natural Sciences, Seoul National University, Seoul 08826, Korea

²Research Institute of Oceanography, Seoul National University, Seoul 08826, Korea

^*Corresponding Author: E-mail: hjjeong@snu.ac.kr, Tel: +82-2-880-6746, Fax: +82-2-874-9695

Present address: CJ CheilJedang Food Research Institute, CJ Blossom Park, Suwon 16495, Korea

Received 2019 July 19; Accepted 2019 August 28.

Abstract

The dinoflagellate genus Alexandrium is known to often form harmful algal blooms causing human illness and large-scale mortality of marine organisms. Therefore, the population dynamics of Alexandrium species are of primary concern to scientists and aquaculture farmers. The growth rate of the Alexandrium species is the most important parameter in prediction models and nutrient conditions are critical parameters affecting the growth of phototrophic species. In Korean coastal waters, Alexandrium affine and Alexandrium fraterculus, of similar sizes, often form red-tide patches together. Thus, to understand bloom dynamics of A. affine and A. fraterculus, growth rates and nitrate uptake of each species as a function of nitrate (NO³) concentration at 100 μmol photons m⁻² s⁻¹ under 14-h light : 10-h dark and continuous light conditions were determined using a nutrient repletion method. With increasing NO³ concentration, growth rates and NO³ uptake of A. affine or A. fraterculus increased, but became saturated. Under light : dark conditions, the maximum growth rates of A. affine and A. fraterculus were 0.45 and 0.42 d⁻¹, respectively. However, under continuous light conditions, the maximum growth rate of A. affine slightly increased to 0.46 d⁻¹, but that of A. fraterculus largely decreased. Furthermore, the maximum nitrate uptake of A. affine and A. fraterculus under light : dark conditions were 12.9 and 30.1 pM cell⁻¹ d⁻¹, respectively. The maximum nitrate uptake of A. affine under continuous light conditions was 16.4 pM cell⁻¹ d⁻¹. Thus, A. affine and A. fraterculus have similar maximum growth rates at the given NO³ concentration ranges, but they have different maximum nitrate uptake rates. A. affine may have a higher conversion rate of NO³ to body nitrogen than A. fraterculus. Moreover, a longer exposure time to the light may confer an advantage to A. affine over A. fraterculus.

Keywords: harmful algal bloom; nitrogen; nutrient; phosphate; protist; red tide

INTRODUCTION

The dinoflagellate genus Alexandrium often forms red tides or harmful algal blooms, causing human illness and large-scale mortality of marine organisms (Anderson et al. 2012). Therefore, the presence and population dynamics of Alexandrium species are primary concerns to scientists and aquaculture farmers (Dias et al. 2015, Eckford-Soper et al. 2016, Hatfield et al. 2019). The growth rate of a red-tide dinoflagellate species is the most important parameter in prediction models of population dynamics (Jeong et al. 2015). Among 34 officially described Alexandrium species, 6–7 species have been revealed to be mixotrophic species (Jacobson and Anderson 1986, Jeong et al. 2005a, 2005b, 2010, Seong et al. 2006, Yoo et al. 2009, Blossom et al. 2012, Lim et al. 2015, Lee et al. 2016). Both exclusively autotrophic and mixotrophic species need nutrients for their growth, and thus nutrient conditions are critical parameters affecting their growth (Yamamoto and Tarutani 1999, Lim et al. 2006, Maguer et al. 2007, Li et al. 2009, Jauzein et al. 2010, Lee et al. 2019). Thus, to understand the population dynamics of an Alexandrium species and to predict the outbreak of red tides or harmful algal blooms by them, growth rates of the species under different nutrient conditions should be determined.

In Korean coastal waters, Alexandrium affine and Alexandrium fraterculus often co-occur (Lee et al. 1998, Kim 2017, our unpublished data). Both species are known to be potentially toxic and also immobilize and/or lyse other protists (Nguyen-Ngoc 2004, Katsuo et al. 2007, Anderson et al. 2012, Basti et al. 2015, Lee et al. 2016, Kang et al. 2018). One or both of these two species usually form red-tide patches before the outbreak of red tides by the ichthyotoxic dinoflagellate Margalefidinium (Cochlodinium) polykrikoides (Jeong et al. 2017). Thus, the population dynamics of A. affine and/or A. fraterculus can be used for predicting the outbreak of M. polykrikoides red tides. Lee et al. (2016) revealed that A. affine and A. fraterculus lacked mixotrophic ability, whereas Alexandrium andersonii had mixotrophic ability. Therefore, nutrient conditions must be critical parameters affecting their growth. Both A. affine and A. fraterculus are known to have worldwide distributions; A. affine has been observed in European, North American, Asian, and Australian waters, while A. fraterculus has been reported to be in North and South American, Australian and New Zealand, and Japanese waters (Fraga et al. 1989, Nakanishi et al. 1996, Moita and Vilarinho 1999, Band-Schmidt et al. 2003, Hansen et al. 2003, Lagos 2003, MacKenzie et al. 2004, Nguyen-Ngoc 2004, Leaw et al. 2005, Omachi et al. 2007, Lee et al. 2009, Nagai et al. 2009, McCarthy 2013, Park et al. 2013). These waters show a wide range of nutrients such as nitrate and phosphate (Fraga et al. 1989, Nogueira et al. 1997, Kang et al. 2019). Furthermore, many phototrophic dinoflagellates can conduct vertical migration (Jeong et al. 2015); they ascend toward well-lit surface waters during the daytime, but descend toward eutrophic deep waters at night. Theoretically, using swimming speed, A. affine and A. fraterculus could be calculated to travel ca. 15–24 m (Lee et al. 2016, Jeong et al. 2017). Thus, they may experience a wide range of nutrient concentrations every day. To understand the population dynamics of A. affine and A. fraterculus, the effects of nutrient concentrations on their growth rates should be explored. The duration of day or night varies depending on latitudes and season (Van Haren and Compton 2013). The duration of light is known to affect the growth of dinoflagellates and other phytoplankton groups (e.g., Brand and Guillard 1981). Thus, it is worthwhile to explore effects of the duration of daytime or night on growth of A. affine and A. fraterculus.

In this present study, growth rates and nitrate uptake of A. affine and A. fraterculus as a function of nitrate concentration at 100 μmol photons m⁻² s⁻¹ under 14-h light : 10-h dark and continuous light conditions were determined using a nutrient repletion method (Lee et al. 2017). The results of the present study provide a basis for understanding ecophysiology of A. affine and A. fraterculus and their bloom dynamics.

MATERIALS AND METHODS

Preparation of experimental organisms

A. affine was isolated from coastal waters off Taean (western Korea) in August 2013 when the water temperature and salinity were 21.5°C and 32.2, respectively (Table 1). A. fraterculus was isolated from Yeosu (southern Korea) in September 2013 when the water temperature and salinity were 23.4°C and 32.8, respectively. Clonal cultures for both species were established from two serial single isolations.

Table 1

Conditions for the isolation of Alexandrium affine and A. fraterculus used in this study

A. affine was grown in enriched f/2-Si seawater medium (Guillard and Ryther 1962), while A. fraterculus was grown in enriched L1-Si seawater medium (Guilliard and Hargraves 1993) at 20°C under an illumination of 20 μmol photons m⁻² s⁻¹ of cool white fluorescent light on a 14-h light : 10-h dark cycle.

Growth and nitrate uptake rates under light and dark conditions

Experiments 1 and 2 were designed to investigate the growth rates and nitrate (NO₃) uptake of A. affine and A. fraterculus as a function of NO₃ concentration under light and dark conditions (Table 2). For this measurement, a nutrient repletion method was used (Lee et al. 2017).

Table 2

Experimental design and the light and nutrient conditions

Dense cultures of A. affine and A. fraterculus, growing in f/2-Si and L1-Si medium, respectively, were transferred to 800-mL culture flasks. The flasks were placed in a culture room at 20°C under 14-h light : 10-h dark cycle and acclimated at 100 μmol photons m⁻² s⁻¹ for 4 d. Three 1-mL aliquots were subsampled and then cells were enumerated to determine the cell concentration. Ten-milliliter aliquots were filtered through GF/F filters (Whatman Inc., Floreham Park, NJ, USA) and then concentrations of NO₃ (actually nitrate + nitrite in the Cd-coil reduction method) and phosphate (PO₄) were measured using a nutrient analyzer (QuAAtro, Seal Analytical, Norderstedt, Germany).

Cells of either species were added to triplicate 800-mL culture flasks by transferring predetermined volumes of cultures (final cell concentration = ~100 cells mL⁻¹ for both species). A stock solution of NO₃ made based on the f/2 medium concentration was added for target final concentrations (NO₃ = ca. 110 μM). A sufficient amount of stock solution of PO₄ (final concentration = ca. 20 μM), also prepared based on the f/2 medium concentration, was added so that it would not be limiting before NO₃ was limiting. Trace metals and vitamins were also added plentifully with consideration of the ratio of nitrate to each chemical in an f/2 medium.

The flasks were placed in a temperature-controlled culture room and incubated at 20°C under an illumination of 100 μmol photons m⁻² s⁻¹ of cool white fluorescent light on a 14-h light : 10-h dark cycle. Thirty-milliliter aliquots were subsampled from each flask every day for 2 weeks, and 10-mL aliquots were used for the determination of cell concentration and 20-mL aliquots for the determination of NO₃ and PO₄ concentrations were filtered through GF/F filters. Cell concentrations (abundances) were determined by enumerating cells on three 1-mL Sedgwick-Rafter counting chambers. The concentrations of nutrients were measured using a nutrient analyzer.

The mean NO₃ concentration (N*) at each interval was calculated as:

(1) N*(μM=[Nt2-Nt1]/[ln(Nt2/Nt1)])

, where N = NO₃ concentration at a single day, t₂ − t₁ = 1 d.

The specific growth rates of each Alexandrium species (μ, d⁻¹) at each N* were calculated as:

(2) μ=[ln(Ct2/Ct1)]/(t2-t1)

, where Ct₁ and Ct₂ = cell concentrations of each Alexandrium species at Day t₁ and Day t₂, respectively.

The maximum growth rate (μ_max, d⁻¹) of each Alexandrium species was obtained after data were fitted to a Michaelis-Menten equation:

(3) μ=μmax[N*/(KGR-NO3+N*)]

,where K_GR-NO3 = the NO₃ concentration sustaining 1/2μ_max.

Data were iteratively fitted to the model using DeltaGraph (SPSS Inc., Chicago, IL, USA).

The daily NO₃ uptake of each Alexandrium cell was determined by dividing the reduction in N* by the mean cell concentration (C*) at 1 d intervals.

(4) (Nt2-Nt1) to (N*t2-N*t1)

(5) C*(cells mL-1)=[Ct2-Ct1]/[ln(Ct2/Ct1)]

, where t₂ − t₁ = 1 d.

Day 0 to 3 for A. affine and Day 0 to 1 for A. fraterculus were treated as the acclimation period, and thus data from these days were not used in calculations. The maximum NO₃ uptake of each Alexandrium species (V, pM cell⁻¹ d⁻¹) was obtained after data were fitted to a Michaelis-Menten equation;

(6) V=Vmax[N*/(KUT-NO3+N*)]

, where V_max = maximum uptake rate (pM cell⁻¹ d⁻¹), N* = mean NO₃ concentration (μM), and K_UT-NO3 = half saturation constant for NO₃ uptake (μM).

The mean PO₄ concentration (P*), specific growth rates of each Alexandrium species at each P*, and daily PO₄ uptake of each cell were calculated in the same manner.

Growth and nitrate uptake rates under continuous light conditions

Experiments 3 and 4 were designed to investigate the growth rates and NO₃ uptake of each of A. affine and A. fraterculus as a function of NO₃ concentrations under continuous light conditions (Table 2). For this measurement, a nutrient repletion method was used (Lee et al. 2017). The procedure of setting up incubating flasks, subsampling, determining cell abundances and nutrient concentrations, and incubation conditions was the same as in experiments 1 and 2 except for the light conditions.

RESULTS

Growth and nitrate uptake rates of Alexandrium affine under light and dark conditions

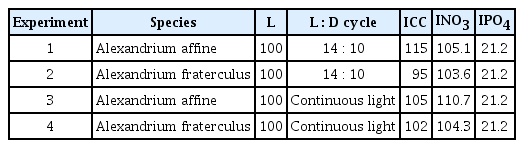
In experiment 1, with increasing incubation time, the concentration of A. affine rapidly increased from 115 cells mL⁻¹ at Day 0 to 5,272 cells mL⁻¹ at Day 10 and then continued to slightly increase (Fig. 1A). The maximum cell concentration (mean ± standard error [SE]) of A. affine concentrations was 7,250 ± 468 cells mL⁻¹ which was achieved at Day 14, the last day of the experiment. The growth rate of A. affine, calculated from linear regression equation, using data between Day 1 and 9, was 0.425 d⁻¹ (Fig. 1B & C). Furthermore, with increasing incubation time, the NO₃ concentration (mean ± SE) rapidly decreased from 105.1 ± 0.4 μM at Day 0 to 11.0 ± 0.6 μM at Day 10 and then became 0.9–1.2 μM at Day 11 to 14 (Fig. 1D). Moreover, with increasing incubation time, the PO₄ concentration (mean ± SE) rapidly decreased from 21.2 ± 0.3 μM at Day 0 to 4.5 ± 0.2 μM at Day 14 (Fig. 1E). With increasing elapsed incubation time, the ratio of NO₃ relative to PO₄ decreased from 5.0–5.3 at Day 0–4 to 2.5 at Day 9 and 0.1–0.2 at Day 11–14 (Fig. 1F).

Fig. 1

(A–C) Change in the concentration (abundance, AB) of Alexandrium affine (cells mL⁻¹) as a function of elapsed time (d) under an illumination of 100 μmol photons m⁻² s⁻¹ on a 14-h light : 10-h dark (LD) cycle. The concentration of A. affine provided in the normal scale (A) and natural log (Ln) scale at Day 0 to 14 (B) and at Day 1 to 9 (C). (D–F) Change in the NO₃ (D) and PO₄ (E) concentrations and ratio of NO₃ relative to PO₄ (F) concentration as a function of elapsed time (d). Symbols represent each treatment. The curves in (B) and (C) are fitted to a linear regression using all the treatments obtained from Day 0 to 14 (B) and from Day 1 to 9 (C). (B) Ln (AB) = 0.332 (d) + 4.89, r² = 0.957; (C) Ln (AB) = 0.425 (d) + 4.50, r² = 0.993.

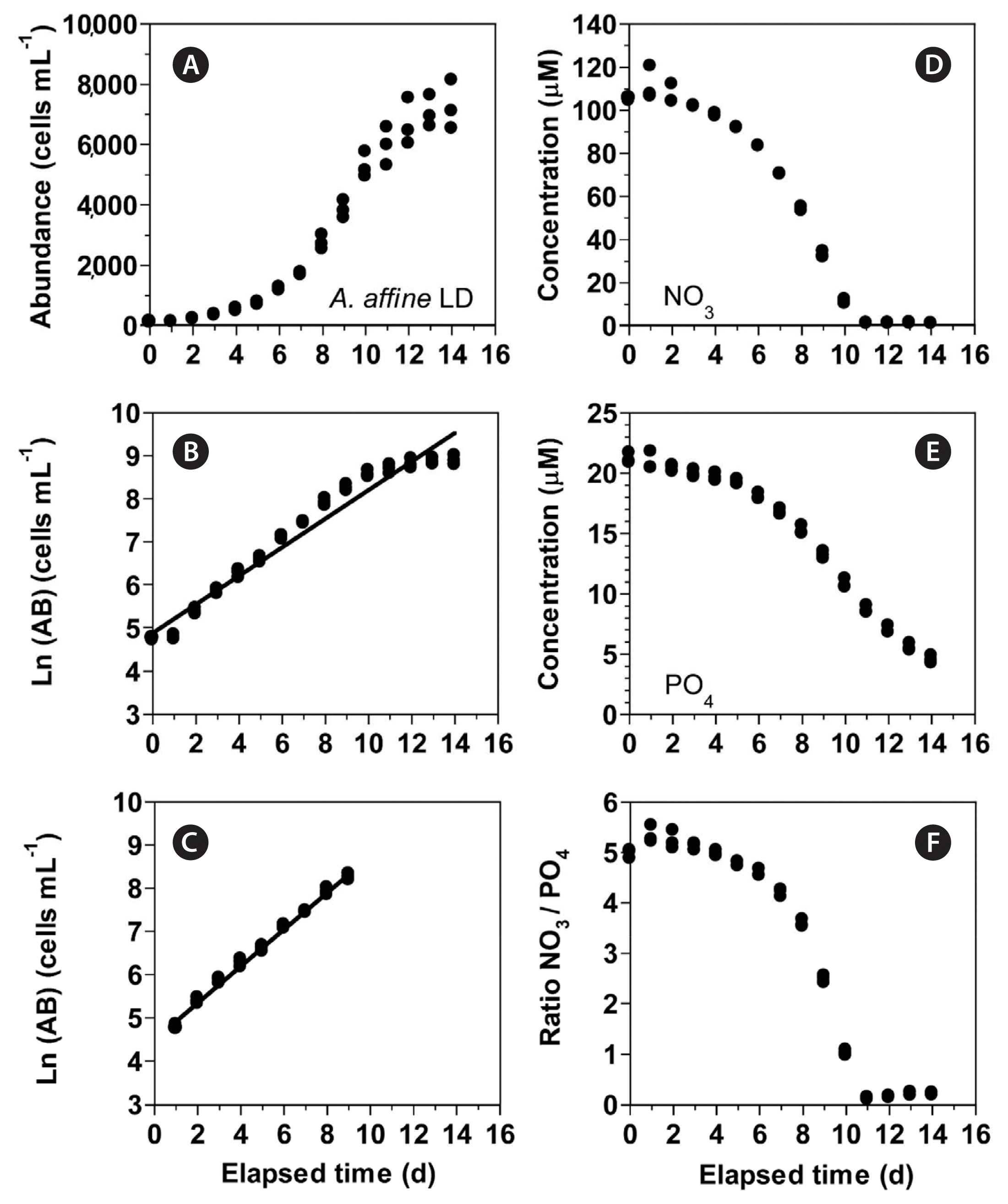
With increasing NO₃ concentration, the growth rate of A. affine rapidly increased and then became saturated (Fig. 2A). When the data were fit to Eq. (3), the maximum growth rate (μ_max) of A. affine was 0.447 d⁻¹ and the half saturation constant for growth rate (K_GR-NO3) was 8.7 μM. However, at the given range of PO₄ concentrations, the growth rate of A. affine linearly increased with increasing PO₄ concentration (Fig. 2B).

Fig. 2

Growth rates (GR, d⁻¹) of Alexandrium affine as a function of NO₃ (A) and PO₄ (B) concentration under an illumination of 100 μmol photons m⁻² s⁻¹ on a 14-h light : 10-h dark (LD) cycle. Symbols represent each treatment. The curve in (A) is fitted to the Michaelis-Menten equation using all the treatments obtained from Day 4 to 14 and that in (B) to a linear regression using all the treatment obtained from Day 4 to 14. (A) GR = 0.447 [NO₃/(8.67 + NO₃)], r² = 0.733; (B) GR = 0.0278 (PO₄) − 0.0934, r² = 0.676.

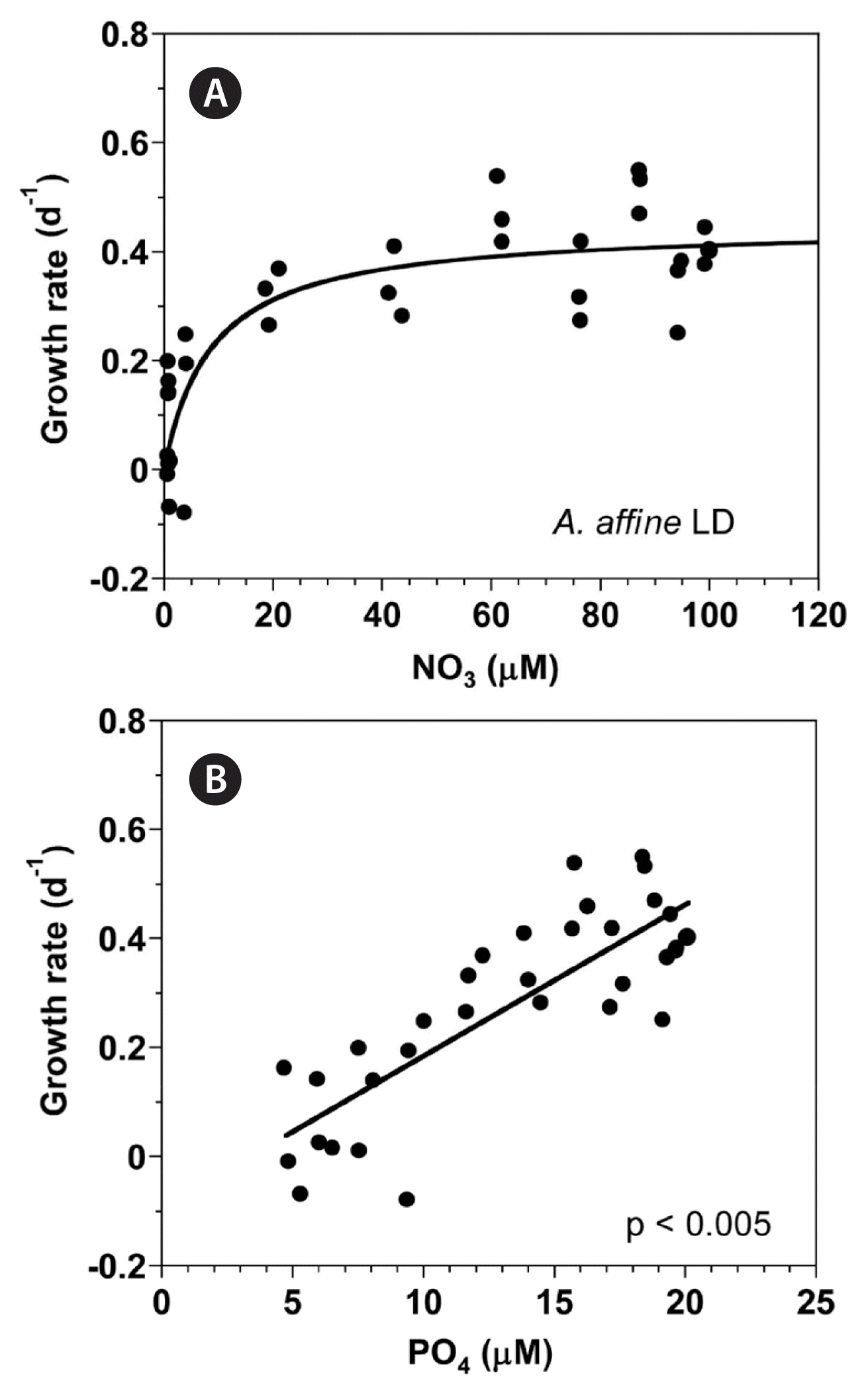
With increasing NO₃ concentration, the NO₃ uptake of A. affine rapidly increased initially, but then increased more slowly (Fig. 3A). When the data were fit to Eq. (4–6), the maximum NO₃ uptake of A. affine was 12.9 pM cell⁻¹ d⁻¹ and the half saturation constant for uptake (K_UT-NO3) was 37.5 μM. However, at the given range of PO₄ concentrations, the PO₄ uptake of A. affine linearly increased with increasing PO₄ concentration (Fig. 3B).

Fig. 3

(A) The NO₃ uptake (NUT, pM cell⁻¹ d⁻¹) of Alexandrium affine as a function of NO₃ concentrations (μM) under an illumination of 100 μmol photons m⁻² s⁻¹ on a 14-h light : 10-h dark (LD) cycle. (B) The PO₄ uptake (PUT, pM cell⁻¹ d⁻¹) of A. affine as a function of PO₄ concentrations (μM). Symbols represent each treatment. The curve in (A) is fitted to the Michaelis-Menten equation using all the treatments obtained from Day 4 to 14 and that in (B) to a linear regression using all the treatment obtained from Day 4 to 14. (A) NUT = 12.9 [NO₃/(37.5 + NO₃)], r² = 0.971; (B) PUT = 0.05 (PO₄) − 0.0887, r² = 0.676.

Growth and nitrate uptake rates of Alexandrium fraterculus under light and dark conditions

In experiment 2, with increasing incubation time, the concentration of A. fraterculus increased from 95 cells mL⁻¹ at Day 0 to ca. 4,350 cells mL⁻¹ at Day 13 and then slightly decreased (Fig. 4A). The growth rate of A. fraterculus calculated from linear regression equation using data between Day 1 and 9 was 0.389 d⁻¹ (Fig. 4B & C). Furthermore, with increasing incubation time, the NO₃ concentration rapidly decreased from 103.6 ± 0.5 μM at Day 0 to 4.2 ± 2.7 μM at Day 9 and then became 0.8–1.3 μM at Day 10 to 14 (Fig. 4D). Moreover, with increasing incubation time, the PO₄ concentration decreased from 21.2 ± 0.2 μM at Day 0 to 11.0 ± 0.2 μM at Day 14 (Fig. 4E). With increasing elapsed incubation time, the ratio of NO₃ relative to PO₄ decreased from 4.9–5.0 at Day 0–2 to 1.5 at Day 8 and 0.1–0.3 at Day 9–14 (Fig. 4F).

Fig. 4

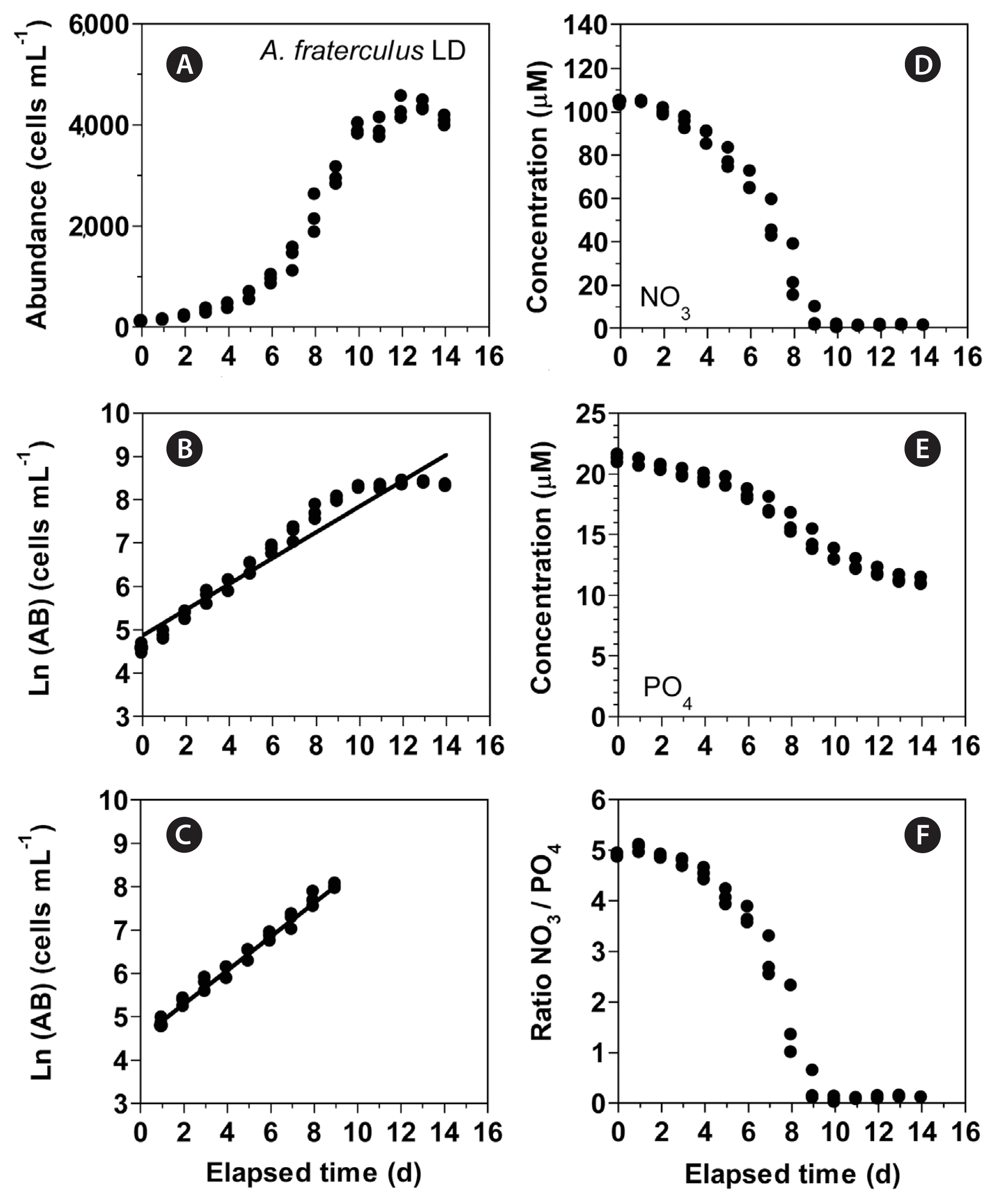
(A–C) Change in the concentration of Alexandrium fraterculus (cells mL⁻¹) as a function of elapsed time (d) under an illumination of 100 μmol photons m⁻² s⁻¹ on a 14-h light : 10-h dark (LD) cycle. The concentration of A. fraterculus provided in the normal scale (A) and natural log (Ln) scale at Day 0 to 14 (B) and at Day 1 to 9 (C). (D–F) Change in the NO₃ (D) and PO₄ (E) concentrations and ratio of NO₃ relative to PO₄ (F) concentration as a function of elapsed time (d). Symbols represent each treatment. The curves in (B) and (C) are fitted to a linear regression using all the treatments obtained from Day 0 to 14 (B) and from Day 1 to 9 (C). (B) Ln (AB) = 0.298 (d) + 4.87, r² = 0.937; (C) Ln (AB) = 0.389 (d) + 4.52, r² = 0.986.

With increasing NO₃ concentration, the growth rate of A. fraterculus rapidly increased and then became saturated (Fig. 5A). When the data were fit to Eq. (3), the maximum growth rate (μ_max) of A. fraterculus was 0.422 d⁻¹ and half saturation constant for growth rate (K_GR-NO3) was 5.4 μM. However, at the given range of PO₄ concentrations, the growth rate of A. fraterculus linearly increased with increasing PO₄ concentration (Fig. 5B).

Fig. 5

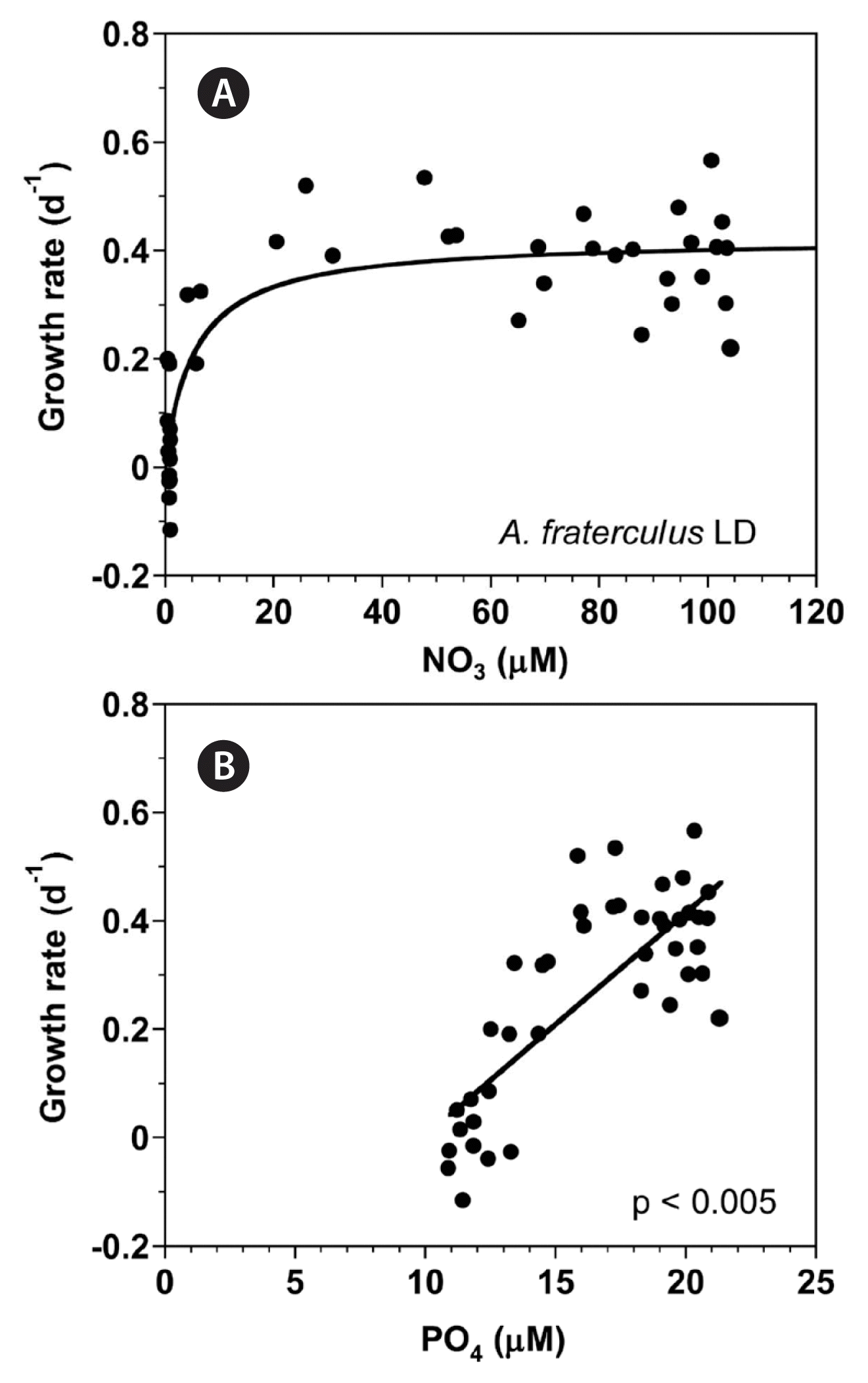
Growth rates (GR, d⁻¹) of Alexandrium fraterculus as a function of NO₃ (A) and PO₄ (B) concentration under an illumination of 100 μmol photons m⁻² s⁻¹ on a 14-h light : 10-h dark (LD) cycle. Symbols represent each treatment. The curve in (A) is fitted to the Michaelis-Menten equation using all the treatments obtained from Day 0 to 14 and that in (B) to a linear regression using all the treatment obtained from Day 0 to 14. (A) GR = 0.422 [NO₃/(5.38 + NO₃)], r² = 0.741; (B) GR = 0.0412 (PO₄) − 0.41, r² = 0.615.

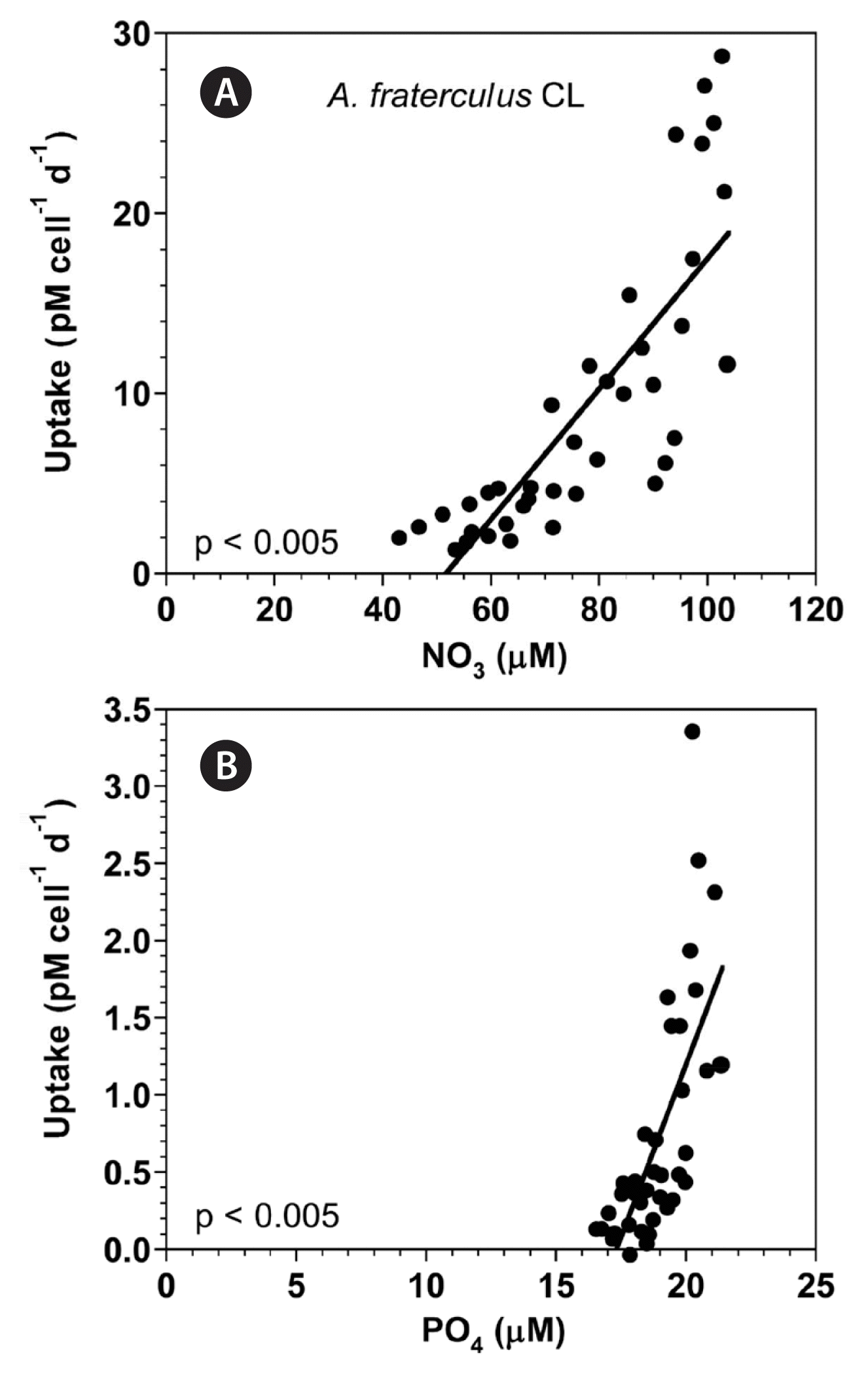
With increasing NO₃ concentration, the NO₃ uptake of A. fraterculus rapidly increased initially, but then increased more slowly (Fig. 6A). When the data were fit to Eq. (4–6), the maximum NO₃ uptake by A. fraterculus was 30.1 pM cell⁻¹ d⁻¹ and the half saturation constant for uptake (K_UT-NO3) was 44.4 μM. However, at the given range of PO₄ concentrations, the PO₄ uptake of A. fraterculus linearly increased with increasing PO₄ concentration (Fig. 6B).

Fig. 6

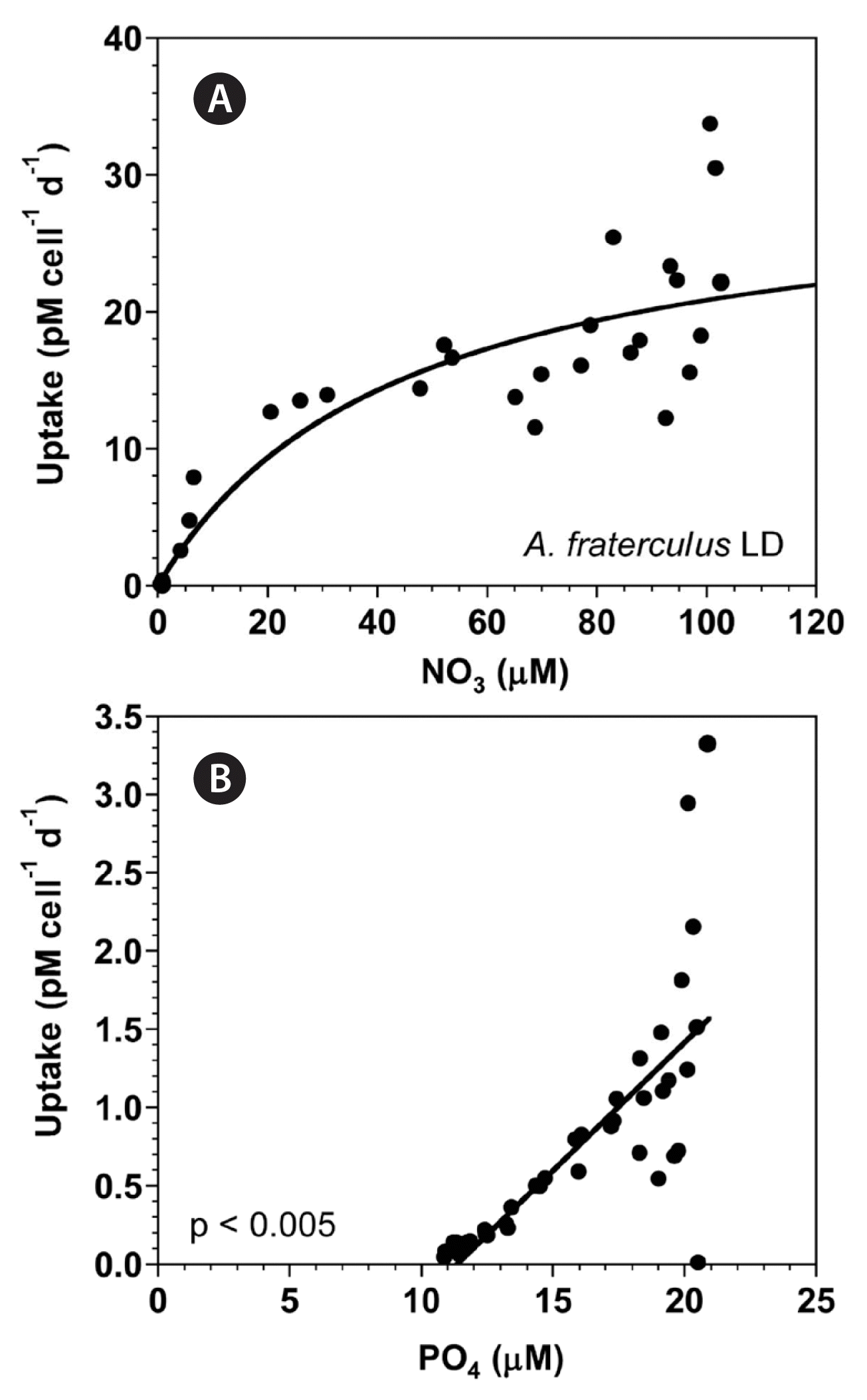
(A) The NO₃ uptake (NUT, pM cell⁻¹ d⁻¹) of Alexandrium fraterculus as a function of NO₃ concentrations (μM) under an illumination of 100 μmol photons m⁻² s⁻¹ on a 14-h light : 10-h dark (LD) cycle. (B) The PO₄ uptake (PUT, pM cell⁻¹ d⁻¹) of A. fraterculus as a function of PO₄ concentrations (μM). Symbols represent each treatment. The curve in (A) is fitted to the Michaelis-Menten equation using all the treatments obtained from Day 2 to 14 and that in (B) to a linear regression using all the treatment obtained from Day 2 to 14. (A) NUT = 30.1 [NO₃/(44.4 + NO₃)], r² = 0.843; (B) PUT = 0.164 (PO₄) − 1.86, r² = 0.548.

Growth and nitrate uptake rates of Alexandrium affine under the continuous light conditions

In experiment 3, with increasing incubation time, the concentration of A. affine rapidly increased from 105 cells mL⁻¹ at Day 0 to 5,779 cells mL⁻¹ at Day 12 and then became saturated (Fig. 7A). The growth rate of A. affine, calculated from a linear regression equation using data between Day 1 and 9, was 0.405 d⁻¹ (Fig. 7B & C). Furthermore, with increasing incubation time, the NO₃ concentration rapidly decreased from 110.7 ± 6.3 μM at Day 0 to 15.7 ± 4.2 μM at Day 11 and then became 1.1–2.6 μM at Day 12 to 14 (Fig. 7D). Moreover, with increasing elapsed incubation time, the PO₄ concentration decreased from 21.2 ± 0.3 μM at Day 0 to 8.4 ± 0.5 μM at Day 14 (Fig. 7E). With increasing incubation time, the ratio of NO₃ relative to PO₄ decreased from 5.0–5.2 at Day 0–5 to 1.3 at Day 11 and 0.1–0.3 at Day 12–14 (Fig. 7F).

Fig. 7

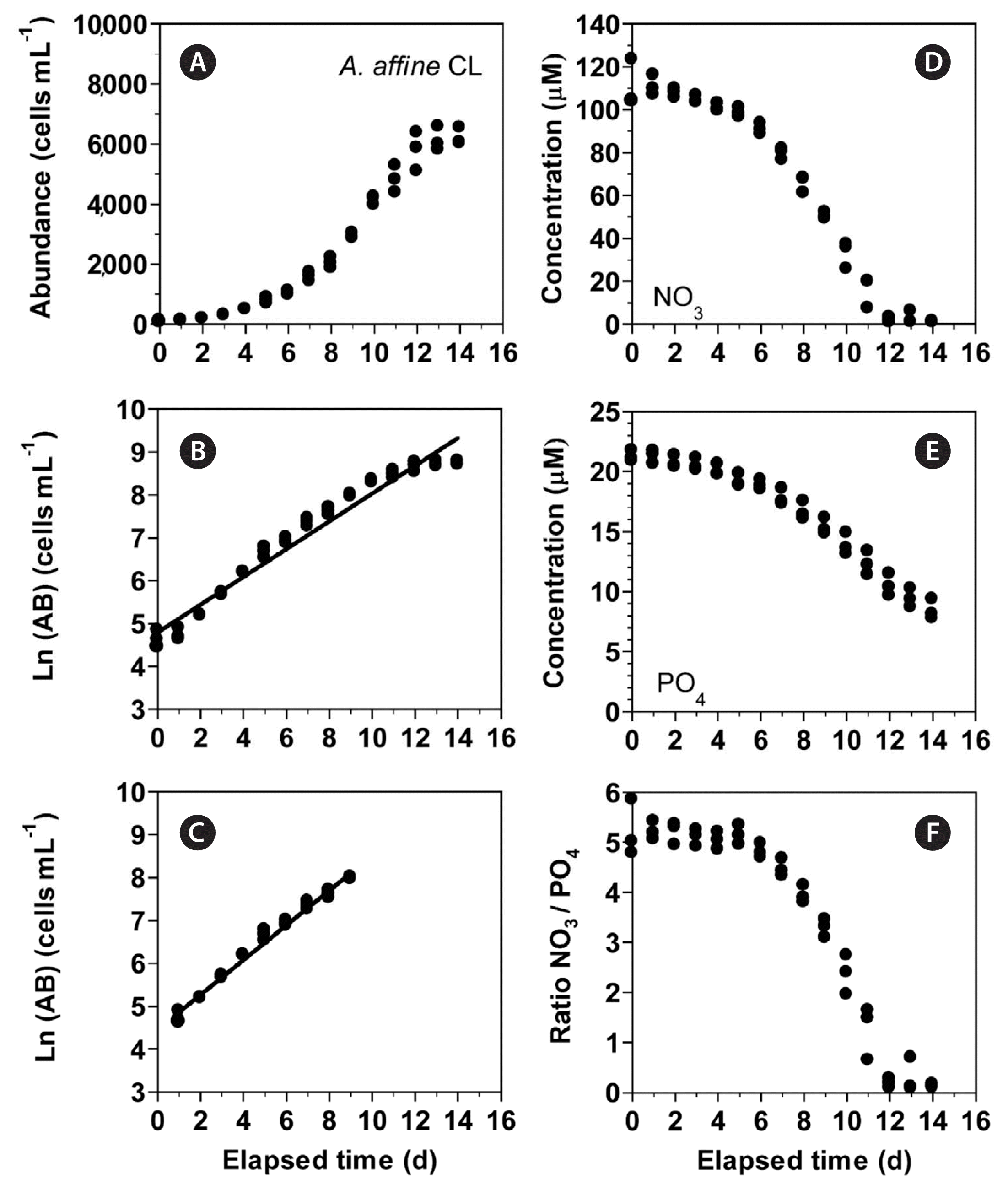
(A–C) Change in the concentration of Alexandrium affine (cells mL⁻¹) as a function of elapsed time (d) at 100 μmol photons m⁻² s⁻¹ under continuous light conditions (CL). The concentration of A. affine provided in the normal scale (A) and natural log (Ln) scale at Day 0 to 14 (B) and at Day 1 to 9 (C). (D–F) Change in the NO₃ (D) and PO₄ (E) concentrations and ratio of NO₃ relative to PO₄ (F) concentration as a function of elapsed time (d). Symbols represent each treatment. The curves in (B) and (C) are fitted to a linear regression using all the treatments obtained from Day 0 to 14 (B) and from Day 1 to 9 (C). (B) Ln (AB) = 0.324 (d) + 4.79, r² = 0.961; (C) Ln (AB) = 0.405 (d) + 4.46, r² = 0.986.

With increasing NO₃ concentration, the growth rate of A. affine rapidly increased and then became saturated (Fig. 8A). When the data were fit to Eq. (3), the maximum growth rate (μ_max) of A. affine was 0.458 d⁻¹ and the half saturation constant for growth rate (K_GR-NO3) was 21.5 μM. However, at the given range of PO₄ concentrations, the growth rate of A. affine linearly increased with increasing PO₄ concentration (Fig. 8B).

Fig. 8

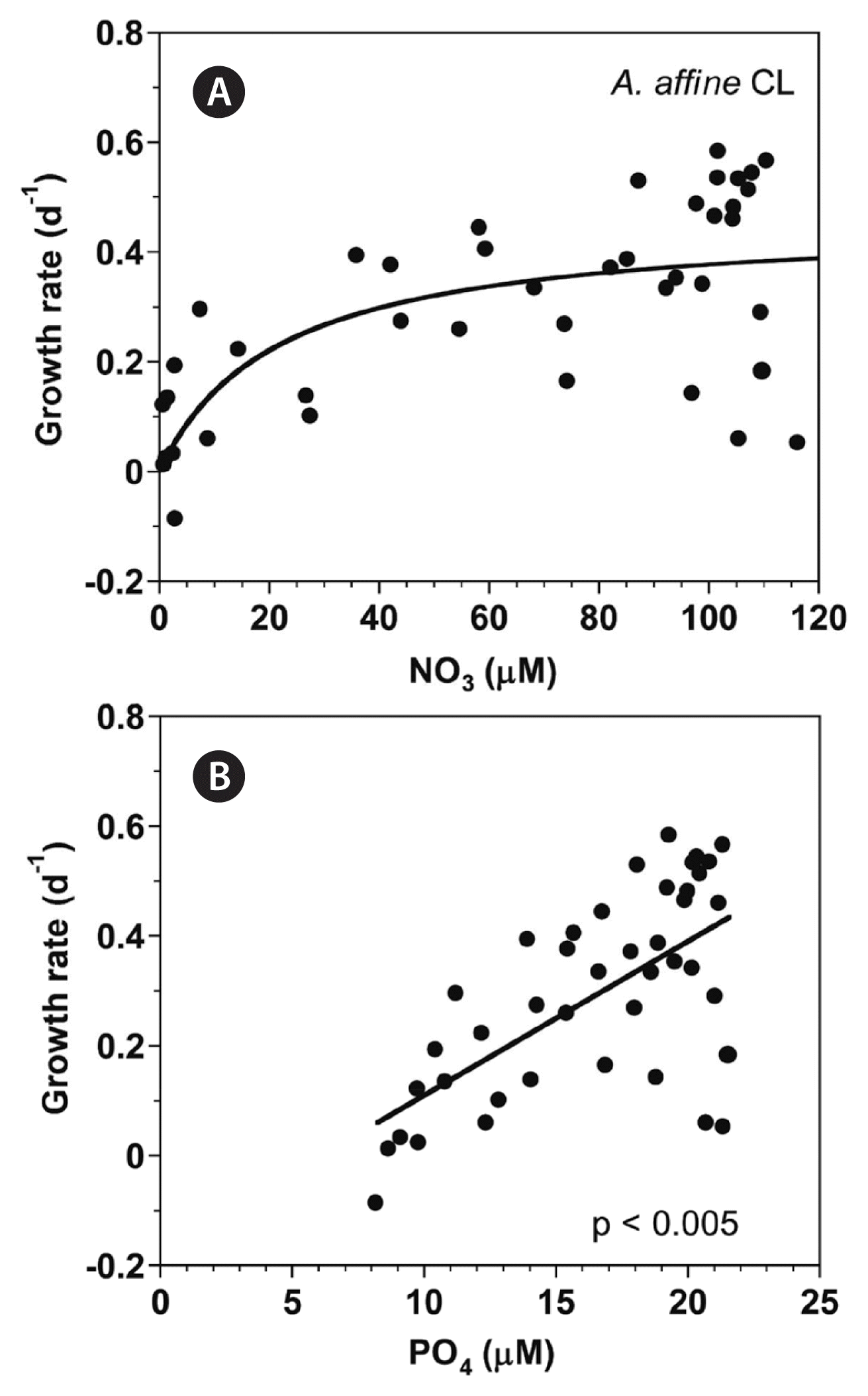
Growth rates (GR, d⁻¹) of Alexandrium affine as a function of NO₃ (A) and PO₄ (B) concentration at 100 μmol photons m⁻² s⁻¹ under continuous light conditions (CL). Symbols represent each treatment. The curve in (A) is fitted to the Michaelis-Menten equation using all the treatments obtained from Day 0 to 14 and that in (B) to a linear regression using all the treatment obtained from Day 0 to 14. (A) GR = 0.458 [NO₃/(21.5 + NO₃)], r² = 0.439; (B) GR = 0.0281 (PO₄) − 0.171, r² = 0.417.

With increasing NO₃ concentration, the NO₃ uptake of A. affine rapidly increased initially, but then increased more slowly (Fig. 9A). When the data were fit to Eq. (4–6), the maximum NO₃ uptake of A. affine was 16.4 pM cell⁻¹ d⁻¹ and half saturation constant for uptake (K_UT-NO3) was 83.3 μM. However, at the given range of PO₄ concentrations, the PO₄ uptake of A. affine linearly increased with increasing PO₄ concentration (Fig. 9B).

Fig. 9

(A) The NO₃ uptake (NUT, pM cell⁻¹ d⁻¹) of Alexandrium affine as a function of NO₃ concentrations (μM) at 100 μmol photons m⁻² s⁻¹ under continuous light conditions (CL). (B) The PO₄ uptake (PUT, pM cell⁻¹ d⁻¹) of A. affine as a function of PO₄ concentrations (μM). Symbols represent each treatment. The curve in (A) is fitted to the Michaelis-Menten equation using all the treatments obtained from Day 3 to 14 and that in (B) to a linear regression using all the treatment obtained from Day 3 to 14. (A) NUT = 16.4 [NO₃/(83.3 + NO₃)], r² = 0.606; (B) PUT = 0.0764 (PO₄) − 0.592, r² = 0.603.

Growth and nitrate uptake rates of Alexandrium fraterculus under the continuous light conditions

In experiment 4, with increasing incubation time, the concentration of A. fraterculus increased from 102 cells mL⁻¹ at Day 0 to 1,587 cells mL⁻¹ at Day 14 (Fig. 10A). The growth rate of A. fraterculus, calculated from linear regression equation using data between Day 2 and 9, was 0.295 d⁻¹ (Fig. 10B & C). Furthermore, with increasing incubation time, the NO₃ concentration decreased from 104.3 ± 0.3 μM at Day 0 to 49.9 ± 4.1 μM at Day 14 (Fig. 10D). Moreover, with increasing incubation time, the PO₄ concentration rapidly decreased from 21.2 ± 0.3 μM at Day 0 to 17.3 ± 0.5 μM at Day 14 (Fig. 10E). With increasing elapsed incubation time, the ratio of NO₃ relative to PO₄ decreased from 4.9–5.0 at Day 0–2 to 2.9 at Day 14 (Fig. 10F).

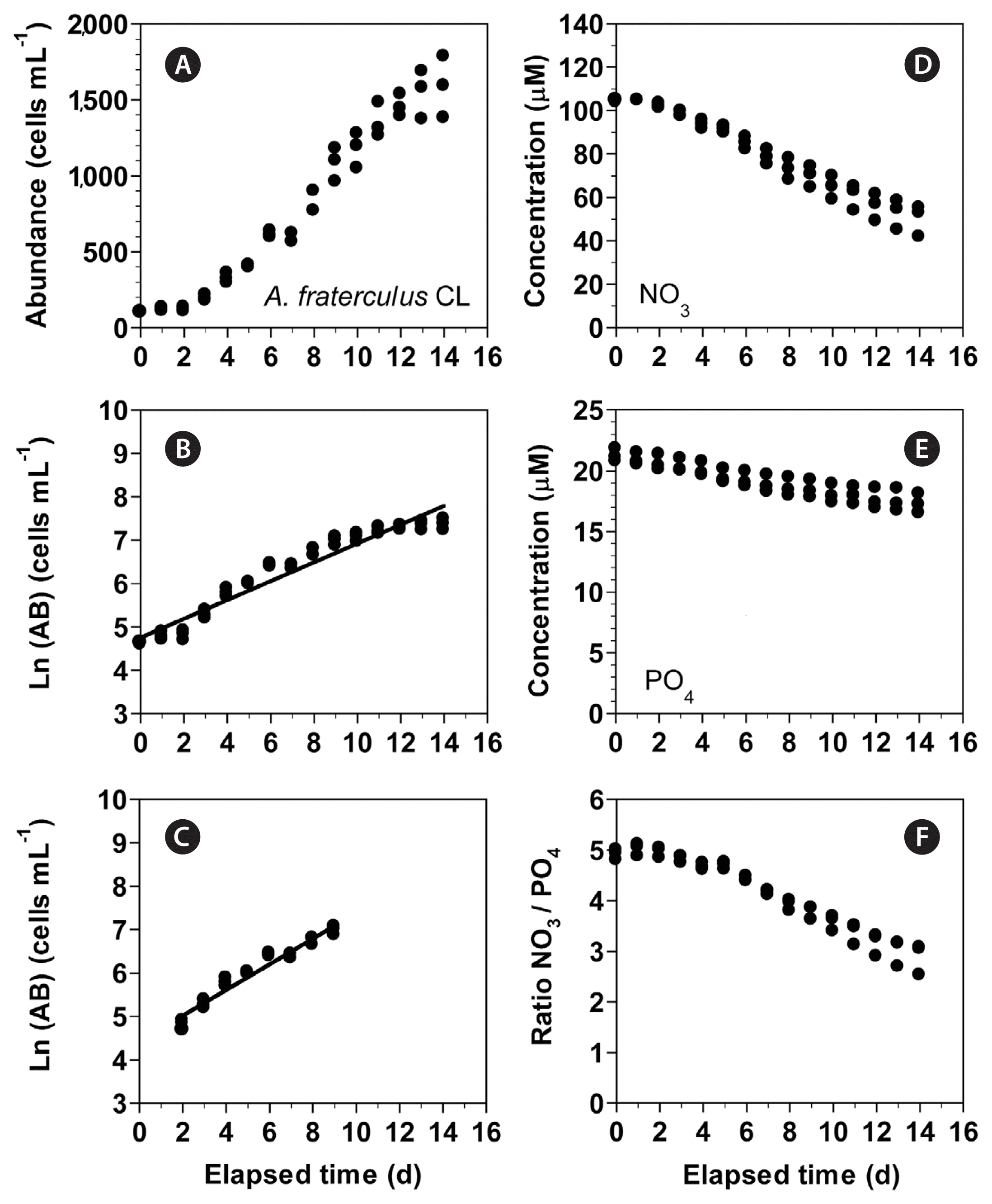
Fig. 10

(A–C) Change in the concentration of Alexandrium fraterculus (cells mL⁻¹) as a function of elapsed time (d) at 100 μmol photons m⁻² s⁻¹ under continuous light conditions (CL). The concentration of A. fraterculus provided in the normal scale (A) and natural log (Ln) scale at Day 0 to 14 (B) and at Day 2 to 9 (C). (D–F) Change in the NO₃ (D) and PO₄ (E) concentrations and ratio of NO₃ relative to PO₄ (F) concentration as a function of elapsed time (d). Symbols represent each treatment. The curves in (B) and (C) are fitted to a linear regression using all the treatments obtained from Day 0 to 14 (B) and from Day 2 to 9 (C). (B) Ln (AB) = 0.217 (d) + 4.75, r² = 0.936; (C) Ln (AB) = 0.295 (d) + 4.43, r² = 0.951.

At the given range of NO₃ concentrations, the growth rate of A. fraterculus linearly increased with increasing NO₃ concentration (Fig. 11A). Also, at the given range of PO₄ concentrations, the growth rate of A. fraterculus linearly increased with increasing PO₄ concentration (Fig. 11B).

Fig. 11

Growth rates (GR, d⁻¹) of Alexandrium fraterculus as a function of NO₃ (A) and PO₄ (B) concentration at 100 μmol photons m⁻² s⁻¹ under continuous light conditions (CL). Symbols represent each treatment. The curve in (A) is fitted to a linear regression using all the treatments obtained from Day 2 to 14 and that in (B) from Day 2 to 14. (A) GR = 0.00508 (NO₃) − 0.193, r² = 0.224; (B) GR = 0.0623 (PO₄) − 0.98, r² = 0.165.

At the given range of NO₃ concentrations, the NO₃ uptake of A. fraterculus linearly increased with increasing NO₃ concentration (Fig. 12A). Furthermore, at the given range of PO₄ concentrations, the PO₄ uptake of A. fraterculus linearly increased with increasing PO₄ concentration (Fig. 12B).

Fig. 12

(A) The NO₃ uptake (NUT, pM cell⁻¹ d⁻¹) of Alexandrium fraterculus as a function of NO₃ concentrations (μM) at 100 μmol photons m⁻² s⁻¹ under continuous light conditions (CL). (B) The PO₄ uptake (PUT, pM cell⁻¹ d⁻¹) of A. fraterculus as a function of PO₄ concentrations (μM). Symbols represent each treatment. The curve in (A) is fitted to a linear regression using all the treatments obtained from Day 2 to 14 and that in (B) from Day 2 to 14. (A) NUT = 0.362 (NO₃) − 18.7, r² = 0.656; (B) PUT = 0.447 (PO₄) − 7.74, r² = 0.502.

DISCUSSION

The growth rate of A. affine at 64 μM, which was the mean NO₃ concentration between Day 1 and 9, calculated using the Michaelis-Menten type equation in Fig. 2A (0.394 d⁻¹), is only 8% different from that calculated using the linear regression equation in Fig. 1C (0.425 d⁻¹). Similarly, the growth rate of A. fraterculus at 31 μM, which was the mean NO₃ concentration between Day 1 and 9, calculated using the Michaelis-Menten type equation in Fig. 5A (0.360 d⁻¹), is also only 8% different from that calculated using the linear regression equation in Fig. 4C (0.389 d⁻¹). Thus, the nutrient repletion method is a reasonable tool for determining growth rates of A. affine and A. fraterculus as a function of NO₃ concentration.

The maximum growth rate of A. affine obtained in the present study is comparable to that reported in Nguyen-Ngoc (2004) and Lim et al. (2019), while the maximum growth rate of A. fraterculus obtained in the present study is slightly higher than Lim et al. (2007) (Table 3). The present study reports for the first time the half saturation constant for growth rate (K_GR-NO3) and for NO₃ uptake (K_UT-NO3) of A. affine and A. fraterculus (Table 3). The values of K_GR-NO3 and K_UT-NO3 are important in understanding competition among red-tide or harmful algal bloom species, because those with lower K_GR-NO3 and K_UT-NO3 can grow and uptake NO₃ rapidly at lower NO₃ concentrations. Furthermore, growth rates and NO₃ uptake of the species largely change when NO₃ concentrations change near K_GR-NO3 and K_UT-NO3. The range of NO₃ concentrations in the waters, collected from April 2015 to October 2018, from Taean (West Sea of Korea) and Yeosu (South Sea of Korea) from which A. affine and A. fraterculus were isolated, were 1.6–10.7 and 0.8–26.4 μM, respectively (Kang et al. 2019). Furthermore, the range of NO₃ concentrations in Junk Bay, Hong Kong and Ria de Vigo, northwest Spain, from which A. affine was found were 0–15.0 and 0–30.0 μM, respectively (Fraga et al. 1989, Nogueira et al. 1997, Hodgkiss and Lu 2004, Lee et al. 2009). The K_GR-NO3 of A. affine (8.7 μM) and A. fraterculus (5.4 μM) fall in the ranges of the NO₃ concentrations in the waters off Taean and Yeosu, Korea, Junk Bay, Hong Kong, and Ria de Vigo, Spain. Therefore, a small change in NO₃ concentrations in these waters may sometimes cause a large change in growth rates of A. affine and A. fraterculus.

Table 3

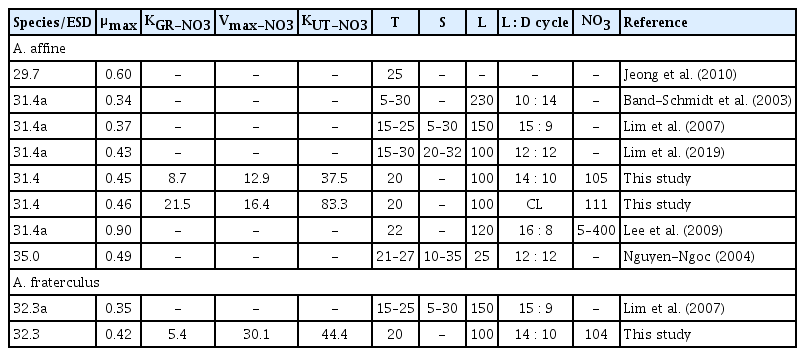
Maximum growth rates (μ_max, d⁻¹) of Alexandrium affine and A. fraterculus, half saturation constant for growth rate as a function of nitrate concentration (K_GR-NO3, μM), nitrate maximum uptake (V_max-NO3, pM cell⁻¹ d⁻¹), half saturation constant for the nitrate uptake as a function of nitrate concentration (K_UT-NO3, μM) and conditions for growth

The range of NO₃ concentrations in the waters, collected from April 2015 to October 2018, from 9 stations located in South Sea of Korea in which A. affine and A. fraterculus have caused red tides or harmful algal blooms, was 0.4–102.9 μM (Kang et al. 2019). Moreover, the range of NO₃ concentrations in Seto Inland Sea, Japan in which A. affine and A. fraterculus were found was 5.4–70.0 μM (Nakanishi et al. 1996, Montani et al. 1998, Nagai et al. 2009). The K_UT-NO3 of A. affine (37.5 μM) and A. fraterculus (44.4 μM) fall in the ranges of the NO₃ concentrations in South Sea of Korea and Seto Inland Sea. Therefore, a small change in NO₃ concentrations in South Sea of Korea and Seto Inland Sea may sometimes cause a large change in the NO₃ uptake of A. affine and A. fraterculus. In addition, the K_UT-NO3 of A. affine was lower than that of A. fraterculus, while the K_GR-NO3 of A. fraterculus was lower than that of A. affine. Therefore, A. affine rapidly uptakes NO₃ at lower NO₃ concentrations than A. fraterculus, but A. fraterculus rapidly grows at lower NO₃ concentrations than A. affine.

Interestingly, the K_GR-NO3 of A. affine and A. fraterculus were much lower than their K_UT-NO3. That is, the growth rates of A. affine and A. fraterculus became saturated at the NO₃ concentrations at which NO₃ uptakes increased. For a cell to divide, the cell should uptake a certain amount of NO₃. Thus, NO₃ acquired by the cell may not have been high enough to be used for cell division. Similar patterns are often observed in feeding by mixotrophic and heterotrophic protists; growth rate of a mixotrophic or heterotrophic protist on algal prey become saturated at prey concentrations at which its ingestion rates increase (Jeong et al. 2007, 2014, 2018a, 2018b, Lim et al. 2014). In conclusion, the values of K_GR-NO3 and K_UT-NO3 of a species should be determined separately because they can be different from each other. The nutrient repletion method can be a useful tool for determining K_GR-NO3 and K_UT-NO3 of the species as a function of NO₃ concentration simultaneously.

The maximum NO₃ uptake of A. affine (ca. 13–16 pM cell⁻¹ d⁻¹) is comparable to that of Alexandrium minutum (4.3–16.8 pM cell⁻¹ d⁻¹) and Alexandrium tamiyavanichii (ca. 10–20 pM cell⁻¹ d⁻¹), but the maximum NO₃ uptake of A. fraterculus (ca. 30 pM cell⁻¹ d⁻¹) is greater than that of these Alexandrium species (Lim et al. 2006, Maguer et al. 2007). The size of A. fraterculus (32.3 μm) is larger than that of A. minimum (20.5 μm), comparable to that of A. affine (31.4 μm), but smaller than that of A. tamiyavanichii (38.6 μm). The maximum NO₃ uptake of these Alexandrium species was not significantly correlated with their size (p > 0.1, linear regression ANOVA). Thus, the maximum NO₃ uptake of an Alexandrium species should be measured because it may not be calculated using the equation of a regression between the maximum NO₃ uptake and size of Alexandrium species.

The maximum growth rate of A. fraterculus under continuous light conditions was much lower than that under light and dark conditions, whereas the maximum growth rate of A. affine grown under continuous light conditions was slightly higher than that under light and dark conditions. This evidence suggests that growth rate of A. fraterculus may be inhibited by continuous light. One scenario is that A. fraterculus has a strong circadian rhythm and a continuous light condition disturbs this rhythm. There have been many dinoflagellates species showing circadian rhythms (Prézelin et al. 1977, Knaust et al. 1998, Van Dolah et al. 2007, Dapena et al. 2015); A. minutum showed nuclear and morphological changes during cell cycle and growth, indicating a strong circadian rhythm (Dapena et al. 2015). In contrast, to our best knowledge, there has only been one dinoflagellate species identified as showing inhibition of growth under a continuous light condition; the growth rate of Tripos (Ceratium) ranipes under a continuous light of 320 μmol photons m⁻² s⁻¹ was much lower than that under light and dark cycle (Brand and Guillard 1981). Thus, the present study adds A. fraterculus to a few dinoflagellate species showing inhibition of growth under a continuous light condition. Another scenario is that an excessive amount of photons inhibits the operation of photosystems of A. fraterculus (Richardson et al. 1983, Krause 1988). The amount of photons produced by a continuous light is ca. 40% greater than that by 14-h illumination. Thus, the amount of photons produced by a continuous light at 100 μmol photons m⁻² s⁻¹ is equivalent to that at 140 μmol photons m⁻² s⁻¹ under 14-h light : 10-h dark cycle. The autotrophic growth of the mixotrophic dinoflagellate Takayama helix is known to be inhibited at 115 μmol photons m⁻² s⁻¹ under 14-h light : 10-h dark cycle (Ok et al. 2019). Therefore, it is worthwhile to explore possible inhibition of growth of A. fraterculus at high light intensities under 14-h light : 10-h dark cycle to test this hypothesis.

ACKNOWLEDGEMENTS

We thank An Suk Lim, Sung Yeon Lee, and Se Hyun Jang for technical support. This research was supported by the Useful Dinoflagellate program of Korea Institute of Marine Science and Technology Promotion (KIMST) funded by the Ministry of Oceans and Fisheries (MOF) and the National Research Foundation (NRF) funded by the Ministry of Science and ICT (NRF-2015M1A5A1041806; NRF-2017R1E1A1A01074419) award to HJJ and (NRF-2019R1C1C1008546) to KHL.

References

Anderson DM, Alpermann TJ, Cembella AD, Collos Y, Masseret E, Montresor M. 2012;The globally distributed genus Alexandrium: multifaceted roles in marine ecosystems and impacts on human health. Harmful Algae 14:10–35.

Band-Schmidt CJ, Lechuga-Devéze CH, Kulis DM, Anderson DM. 2003;Culture studies of Alexandrium affine (Dinophyceae), a non-toxic cyst forming dinoflagellate from Bahía Concepción, Gulf of California. Bot Mar 46:44–54.

Basti L, Nagai S, Go J, Okano S, Nagai K, Watanabe R, Suzuki T, Tanaka Y. 2015;Differential inimical effects of Alexandrium spp. and Karenia spp. on cleavage, hatching, and two larval stages of Japanese pearl oyster Pinctada fucata martensii . Harmful Algae 43:1–12.

Blossom HE, Daugbjerg N, Hansen PJ. 2012;Toxic mucus traps: a novel mechanism that mediates prey uptake in the mixotrophic dinoflagellate Alexandrium pseudogonyaulax . Harmful Algae 17:40–53.

Brand LE, Guillard RRL. 1981;The effects of continuous light and light intensity on the reproduction rates of twenty-two species of marine phytoplankton. J Exp Mar Biol Ecol 50:119–132.

Dapena C, Bravo I, Cuadrado A, Figueroa RI. 2015;Nuclear and cell morphological changes during the cell cycle and growth of the toxic dinoflagellate Alexandrium minutum . Protist 166:146–160.

Dias J, Muñoz J, Huisman J, McDonald J. 2015;Biosecurity monitoring of Harmful Algal Bloom (HAB) species in Western Australian waters: first confirmed record of Alexandrium catenella (Dinophyceae). Bioinvasions Rec 4:233–241.

Eckford-Soper LK, Bresnan E, Lacaze J-P, Green DH, Davidson K. 2016;The competitive dynamics of toxic Alexandrium fundyense and non-toxic Alexandrium tamarense: the role of temperature. Harmful Algae 53:135–144.

Fraga S, Gallager SM, Anderson DM. 1989. Chain-forming dinoflagellates: an adaptation to red tides. In : Okaichi T, Anderson DM, Nemoto T, eds. Red Tides: Biology, Environmental Science and Toxicology Elsevier. New York: p. 281–284.

Guillard RRL, Hargraves PE. 1993; Stichochrysis immobilis is a diatom, not a chrysophyte. Phycologia 32:234–236.

Guillard RRL, Ryther JH. 1962;Studies of marine planktonic diatoms. I. Cyclotella nana Hustedt and Detonula confervacea (Cleve) Gran. Can J Microbiol 8:229–239.

Hansen G, Daugbjerg N, Franco JM. 2003;Morphology, toxin composition and LSU rDNA phylogeny of Alexandrium minutum (Dinophyceae) from Denmark, with some morphological observations on other European strains. Harmful Algae 2:317–335.

Hatfield RG, Bean T, Turner AD, Lees DN, Lowther J, Lewis A, Baker-Austin C. 2019;Development of a TaqMan qPCR assay for detection of Alexandrium spp. and application to harmful algal bloom monitoring. Toxicon X 2:100011.

Hodgkiss IJ, Lu S. 2004. The effects of nutrients and their ratios on phytoplankton abundance in Junk Bay, Hong Kong. In : Ang PO, ed. Asian Pacific Phycology in the 21st Century: Prospects and Challenges Springer. Dordrecht: p. 215–229.

Jacobson DM, Anderson DM. 1986;Thecate heterotrophic dinoflagellates: feeding behavior and mechanisms. J Phycol 22:249–258.

Jauzein C, Labry C, Youenou A, Quéré J, Delmas D, Collos Y. 2010;Growth and phosphorus uptake by the toxic dinoflagellate Alexandrium catenella (Dinophyceae) in response to phosphate limitation. J Phycol 46:926–936.

Jeong HJ, Kang HC, You JH, Jang SH. 2018a;Interactions between the newly described small- and fast-swimming mixotrophic dinoflagellate Yihiella yeosuensis and common heterotrophic protists. J Eukaryot Microbiol 65:612–626.

Jeong HJ, Kim JS, Song JY, Kim JH, Kim TH, Kim SK, Kang NS. 2007;Feeding by protists and copepods on the heterotrophic dinoflagellates Pfiesteria piscicida, Stoeckeria algicida, and Luciella masanensis . Mar Ecol Prog Ser 349:199–211.

Jeong HJ, Lim AS, Franks PJS, Lee KH, Kim JH, Kang NS, Lee MJ, Jang SH, Lee SY, Yoon EY, Park JY, Yoo YD, Seong KA, Kwon JE, Jang TY. 2015;A hierarchy of conceptual models of red-tide generation: nutrition, behavior, and biological interactions. Harmful Algae 47:97–115.

Jeong HJ, Lim AS, Lee K, Lee MJ, Seong KA, Kang NS, Jang SH, Lee KH, Lee SY, Kim MO, Kim JH, Kwon JE, Kang HC, Kim JS, Yih W, Shin K, Jang PK, Ryu J-H, Kim SY, Park JY, Kim KY. 2017;Ichthyotoxic Cochlodinium polykrikoides red tides offshore in the South Sea, Korea in 2014: I. temporal variations in three-dimensional distributions of red-tide organisms and environmental factors. Algae 32:101–130.

Jeong HJ, Lim AS, Yoo YD, Lee MJ, Lee KH, Jang TY, Lee K. 2014;Feeding by heterotrophic dinoflagellates and ciliates on the free-living dinoflagellate Symbiodinium sp. (Clade E). J Eukaryot Microbiol 61:27–41.

Jeong HJ, Park JY, Nho JH, Park MO, Ha JH, Seong KA, Jeng C, Seong CN, Lee KY, Yih WH. 2005a;Feeding by red-tide dinoflagellates on the cyanobacterium Synechococcus . Aquat Microb Ecol 41:131–143.

Jeong HJ, Yoo YD, Kim JS, Seong KA, Kang NS, Kim TH. 2010;Growth, feeding, and ecological roles of the mixotrophic and heterotrophic dinoflagellates in marine planktonic food webs. Ocean Sci J 45:65–91.

Jeong HJ, Yoo YD, Park JY, Song JY, Kim ST, Lee SH, Kim KY, Yih WH. 2005b;Feeding by the phototrophic red-tide dinoflagellates: five species newly revealed and six species previously known to be mixotrophic. Aquat Microb Ecol 40:133–150.

Jeong HJ, You JH, Lee KH, Kim SJ, Lee SY. 2018b;Feeding by common heterotrophic protists on the mixotrophic alga Gymnodinium smaydae (Dinophyceae), one of the fastest growing dinoflagellates. J Phycol 54:734–743.

Kang HC, Jeong HJ, Kim SJ, You JH, Ok JH. 2018;Differential feeding by common heterotrophic protists on 12 different Alexandrium species. Harmful Algae 78:106–117.

Kang HC, Jeong HJ, Ok JH, You JH, Jang SH, Lee SY, Lee KH, Park JY, Rho J-R. 2019;Spatial and seasonal distributions of the phototrophic dinoflagellate Biecheleriopsis adriatica (Suessiaceae) in Korea: quantification using qPCR. Algae 34:111–126.

Katsuo D, Kim D, Yamaguchi K, Matsuyama Y, Oda T. 2007;A new simple screening method for the detection of cytotoxic substances produced by harmful red tide phytoplankton. Harmful Algae 6:790–798.

Kim JH. 2017. Spatiotemporal distribution and a survival strategy of harmful dinoflagellates Alexanderium spp. in Korean coastal waters and application to controlling scuticociliates. MS thesis Seoul National University; Seoul, Korea: 136.

Knaust R, Urbig T, Li L, Taylor W, Hastings JW. 1998;The circadian rhythm of bioluminescence in Pyrocystis is not due to differences in the amount of luciferase: a comparative study of three bioluminescent marine dinoflagellates. J Phycol 34:167–172.

Krause GH. 1988;Photoinhibition of photosynthesis: an evaluation of damaging and protective mechanisms. Physiol Plant 74:566–574.

Lagos N. 2003;Paralytic shellfish poisoning phycotoxins: occurrence in South America. Comments Toxicol 9:175–193.

Leaw CP, Lim PT, Ng BK, Cheah MY, Ahmad A, Usup G. 2005;Phylogenetic analysis of Alexandrium species and Pyrodinium bahamense (Dinophyceae) based on theca morphology and nuclear ribosomal gene sequence. Phycologia 44:550–565.

Lee FW, Morse D, Lo SC-L. 2009;Identification of two plastid proteins in the dinoflagellate Alexandrium affine that are substantially down-regulated by nitrogen-depletion. J Proteome Res 8:5080–5092.

Lee J, Kim DY, Lee J. 1998;Community dynamics and distribution of dinoflagellates and their cysts in Masan-Chinhae Bay, Korea. Fish Aquat Sci 1:283–292.

Lee KH, Jeong HJ, Kim HJ, Lim AS. 2017;Nitrate uptake of the red tide dinoflagellate Prorocentrum micans measured using a nutrient repletion method: effect of light intensity. Algae 32:139–153.

Lee KH, Jeong HJ, Kwon JE, Kang HC, Kim JH, Jang SH, Park JY, Yoon EY, Kim JS. 2016;Mixotrophic ability of the phototrophic dinoflagellates Alexandrium andersonii, A. affine, and A. fraterculus . Harmful Algae 59:67–81.

Lee KH, Jeong HJ, Lee K, Franks PJS, Seong KA, Lee SY, Lee MJ, Jang SH, Potvin E, Lim AS, Yoon EY, Yoo YD, Kang NS, Kim KY. 2019;Effects of warming and eutrophication on coastal phytoplankton production. Harmful Algae 81:106–118.

Li T, Yu R, Zhou M-J. 2009;Demand and adsorption strategies of phosphorus of Alexandrium catenella isolated from East China Sea. Mar Environ Sci 28:355–359.

Lim AS, Jeong HJ, Jang TY, Yoo YD, Kang NS, Yoon EY, Kim GH. 2014;Feeding by the newly described heterotrophic dinoflagellate Stoeckeria changwonensis: a comparison with other species in the family Pfiesteriaceae. Harmful Algae 36:11–21.

Lim AS, Jeong HJ, Kim JH, Jang SH, Lee MJ, Lee K. 2015;Mixotrophy in the newly described dinoflagellate Alexandrium pohangense: a specialist for feeding on the fast-swimming ichthyotoxic dinoflagellate Cochlodinium polykrikoides . Harmful Algae 49:10–18.

Lim P-T, Leaw C-P, Kaga S, Sekiguchi K, Ogata T. 2007;Growth responses of five non toxic Alexandrium species (dinophyceae) to temperature and salinity. Mar. Res. Indonesia 32:189–195.

Lim P, Leaw C, Usup G, Kobiyama A, Koike K, Ogata T. 2006;Effects of light and temperature on growth, nitrate uptake, and toxin production of two tropical dinofagellates: Alexandrium tamiyavanichii and Alexandrium minutum (Dinophyceae). J Phycol 42:786–799.

Lim YK, Baek SH, Lee M, Kim YO, Choi K, Kim JH. 2019;Phytoplankton composition associated with physical and chemical variables during summer in the southern sea of Korea: implication of the succession of the two toxic dinoflagellates Cochlodinium (a.k.a. Margalefidinium) polykrikoides and Alexandrium affine . J Exp Mar Biol Ecol 516:51–66.

MacKenzie L, de Salas M, Adamson J, Beuzenberg V. 2004;The dinoflagellate genus Alexandrium (Halim) in New Zealand coastal waters: comparative morphology, toxicity and molecular genetics. Harmful Algae 3:71–92.

Maguer J, L’Helguen S, Madec C, Labry C, Le Corre P. 2007;Nitrogen uptake and assimilation kinetics in Alexandrium minutum (Dynophyceae): effect of N-limited growth rate on nitrate and ammonium interactions. J Phycol 43:295–303.

McCarthy PM. 2013. Census of Australian Marine Dinoflagellates Available from: http://www.anbg.gov.au/abrs/Dinoflagellates/index_Dino.html . Accessed Apr 5, 2019.

Moita MT, Vilarinho MG. 1999;Checklist of phytoplankton species off Portugal: 70 years 1929–1998 of studies. Port Acta Biol Sér B Sist 18:5–50.

Montani S, Magni P, Shimamoto M, Abe N, Okutani K. 1998;The effect of a tidal cycle on the dynamics of nutrients in a tidal estuary in the Seto Inland Sea, Japan. J Oceanogr 54:65–76.

Nagai S, Nishitani G, Takano Y, Yoshida M, Takayama H. 2009;Encystment and excystment under laboratory conditions of the nontoxic dinoflagellate Alexandrium fraterculus (Dinophyceae) isolated from the Seto Inland Sea, Japan. Phycologia 48:177–185.

Nakanishi K, Masao A, Sako Y, Ishida Y, Muguruma H, Karube I. 1996;Detection of the red tide-causing plankton Alexandrium affine by a piezoelectric immunosensor using a novel method of immobilizing antibodies. Anal Lett 29:1247–1258.

Nguyen-Ngoc L. 2004;An autecological study of the potentially toxic dinoflagellate Alexandrium affine isolated from Vietnamese waters. Harmful Algae 3:117–129.

Nogueira E, Pérez FF, Ríos AF. 1997;Seasonal patterns and long-term trends in an estuarine upwelling ecosystem (Ría de Vigo, NW Spain). Estuar Coast Shelf Sci 44:285–300.

Ok JH, Jeong HJ, Lim AS, You JH, Kang HC, Kim SJ, Lee SY. 2019;Effects of light and temperature on the growth of Takayama helix (Dinophyceae): mixotrophy as a survival strategy against photoinhibition. J Phycol Advanced online publication. https://doi.org/10.1111/jpy.12907 .

Omachi CY, Tamanaha MDS, Proença LADO. 2007;Bloom of Alexandrium fraterculus in coastal waters off Itajaí, SC, Southern Brazil. Braz J Oceanogr 55:57–61.

Park J, Jeong HJ, Yoo YD, Yoon EY. 2013;Mixotrophic dinoflagellate red tides in Korean waters: distribution and ecophysiology. Harmful Algae 30(Suppl 1):S28–S40.

Prézelin BB, Meeson BW, Sweeney BM. 1977;Characterization of photosynthetic rhythms in marine dinoflagellates: I. Pigmentation, photosynthetic capacity and respiration. Plant Physiol 60:384–387.

Richardson K, Beardall J, Raven JA. 1983;Adaptation of unicellular algae to irradiance: an analysis of strategies. New Phytol 93:157–191.

Seong KA, Jeong HJ, Kim S, Kim GH, Kang JH. 2006;Bacterivory by co-occurring red-tide algae, heterotrophic nanoflagellates, and ciliates. Mar Ecol Prog Ser 322:85–97.

Van Dolah FM, Lidie KB, Morey JS, Brunelle SA, Ryan JC, Monroe EA, Haynes BL. 2007;Microarray analysis of diurnal-and circadian-regulated genes in the florida red-tide dinoflagellate Karenia brevis (Dinophyceae) 1. J Phycol 43:741–752.

Van Haren H, Compton TJ. 2013;Diel vertical migration in deep sea plankton is finely tuned to latitudinal and seasonal day length. PLoS One 8:e64435.

Yamamoto T, Tarutani K. 1999;Growth and phosphate uptake kinetics of the toxic dinoflagellate Alexandrium tamarense from Hiroshima Bay in the Seto Inland Sea, Japan. Phycol Res 47:27–32.

Yoo YD, Jeong HJ, Kim MS, Kang NS, Song JY, Shin W, Kim KY, Lee KT. 2009;Feeding by phototrophic red-tide dinoflagellates on the ubiquitous marine diatom Skeletonema costatum . J Eukaryot Microbiol 56:413–420.

Article information Continued

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Species	Strain name	ESD	Location	Time	T	S
Alexandrium affine	AATA1308	31.4	Taean, Korea	Aug 2013	21.5	32.2
Alexandrium fraterculus	AFYS1309	32.3	Yeosu, Korea	Sep 2013	23.4	32.8

Experiment	Species	L	L : D cycle	ICC	INO₃	IPO₄
1	Alexandrium affine	100	14 : 10	115	105.1	21.2
2	Alexandrium fraterculus	100	14 : 10	95	103.6	21.2
3	Alexandrium affine	100	Continuous light	105	110.7	21.2
4	Alexandrium fraterculus	100	Continuous light	102	104.3	21.2

Species/ESD	μ_max	K_GR-NO3	V_max-NO3	K_UT-NO3	T	S	L	L : D cycle	NO₃	Reference
A. affine
29.7	0.60	-	-	-	25	-	-	-	-	Jeong et al. (2010)
31.4a	0.34	-	-	-	5–30	-	230	10 : 14	-	Band-Schmidt et al. (2003)
31.4a	0.37	-	-	-	15–25	5–30	150	15 : 9	-	Lim et al. (2007)
31.4a	0.43	-	-	-	15–30	20–32	100	12 : 12	-	Lim et al. (2019)
31.4	0.45	8.7	12.9	37.5	20	-	100	14 : 10	105	This study
31.4	0.46	21.5	16.4	83.3	20	-	100	CL	111	This study
31.4a	0.90	-	-	-	22	-	120	16 : 8	5–400	Lee et al. (2009)
35.0	0.49	-	-	-	21–27	10–35	25	12 : 12	-	Nguyen-Ngoc (2004)
A. fraterculus
32.3a	0.35	-	-	-	15–25	5–30	150	15 : 9	-	Lim et al. (2007)
32.3	0.42	5.4	30.1	44.4	20	-	100	14 : 10	104	This study